O que é GravitaSim?
GravitaSim é uma pequena aplicação que simula graficamente a lei universal da gravidade.
É um simulador gratuito de plataforma múltipla, em 3D que contém vários cenários, reais ou fictícios, onde são colocados objectos com massas e velocidades. Estes interagem entre si usando a lei da gravidade.
Entre os cenários reais, incluem-se o do nosso próprio sistema solar. Neste cenário em particular, a massa dos objectos, coordenadas e vectores de velocidade, são recolhidos da NASA através do Jet Propulsion Laboratory.
Todos cenários podem ser alterados ou adicionados novos, modificando os ficheiros existentes ou criando outros ficheiros.
Este simulador é programado em C++ (mais precisamente C com classes), é freeware, não contém publicidade nem spyware ou qualquer outra forma de monitorização dos utilizadores.
Está disponível para as versões Windows, Linux e macOS e será um projecto em evolução.
Requisitos mínimos de hardware recomendados
Processador : Processador Intel ou AMD com suporte de 64-bit e pelo menos 2 núcleos (ou Apple equivalente).Memória : 512MB memória livre (dependendo do cenário).
Placa Gráfica : Compatível com OpenGL
Resolução do ecrã: 1280 x 1024
Espaço em disco : 150MB
GravitaSim é compilado nas plataformas Linux, Windows e macOS. Deverá portanto correr em qualquer deste sistemas operativos.
Foi testado com sucesso em :
| Windows x86-64Bits: | 7, 8, 10, 11 |
| Linux x86-64Bits: | Debian 11.5.0 Bullseye |
| Ubuntu 22.04.1 | |
| Oracle Linux 9.0 | |
| MacOS AArch64 / x86-64: | Monterey |
| Sonoma |
Instalação
Windows e Linux:
O software GravitaSim corre sem necessidade de instalação. Pode ser executado de uma drive externa, na cloud ou no disco local.
Fazer o download do ficheiro comprimido. Descomprimir o ficheiro para uma pasta à sua escolha e executar a aplicação.
Em alguns sistemas tipo Unix, talvez seja necessário correr a aplicação a partir do terminal.
Para desinstalar, apague a pasta onde está a aplicação.
macOS :
Faça o Download do ficheiro dmg e abra-o.
Para instalar a aplicação arrastar "GravitaSim.app" para a pasta das aplicações. GravitaSim está agora instalado e deverá estar disponível no Launchpad.
Depois de instalado, pode ejectar e apagar o ficheiro dmg descarregado.
Para desinstalar a aplicação, arraste "GravitaSim.app" da pasta das aplicações para
o lixo e apague a pasta GravitaSim que contém os cenários e as definições na pasta dos Downloads.
Imagens de cenários gravitacionais
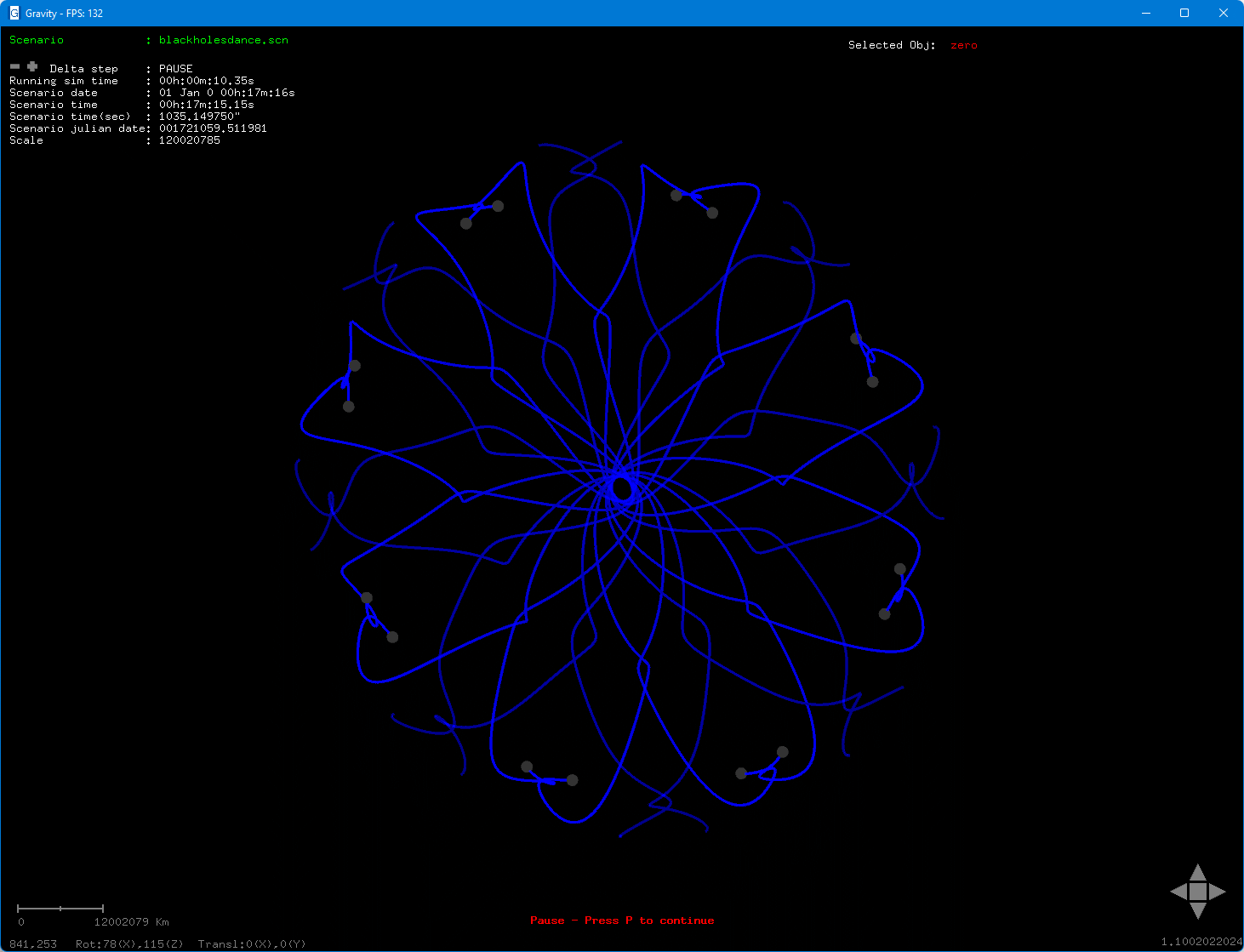
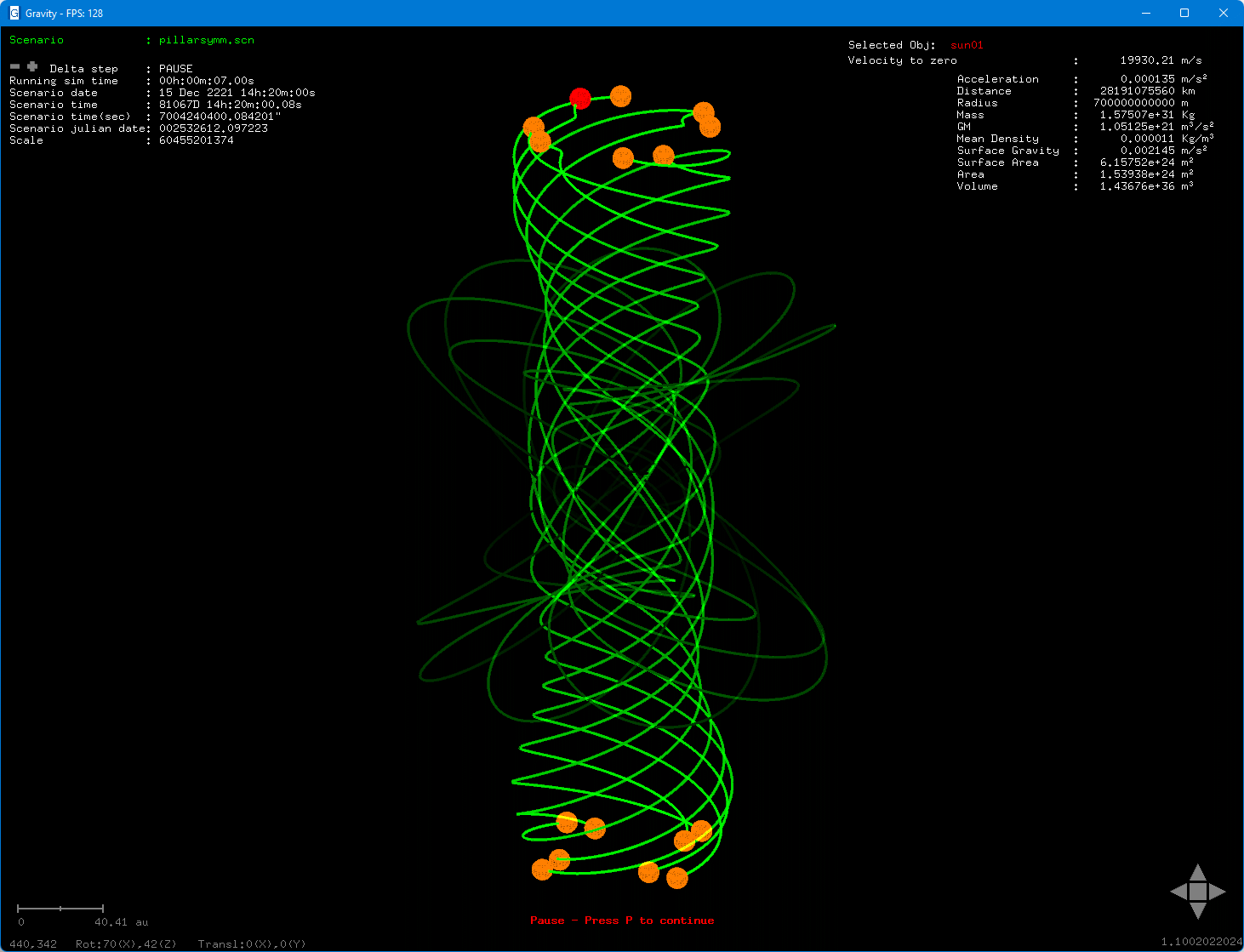
GravitaSim pode ser usado de uma forma recreativa, onde são desenhando padrões mais ou menos complexos como estes buracos negros atraindo-se mutuamente e movendo-se simetricamente ou como na figura seguinte, as estrelas com as trajectórias verdes.
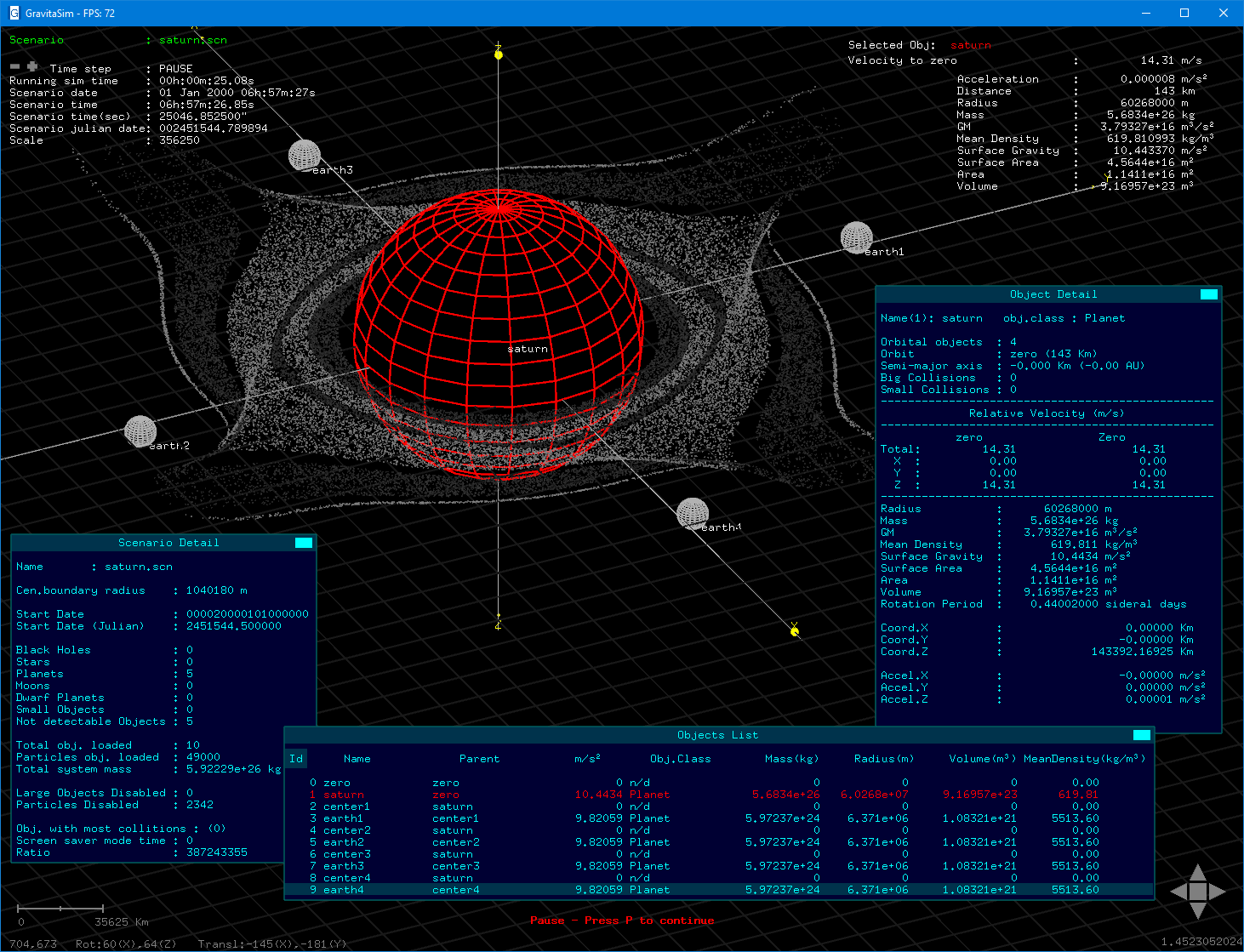
Ou pode ser usado de uma forma mais descritiva onde podem ser analisados os dados gravitacionais referentes aos objectos colocados no cenário. Como estes quatro planetas de tamanho e massa igual à Terra, passando por Saturno e perturbando os seus anéis.
O nosso Sistema Solar.
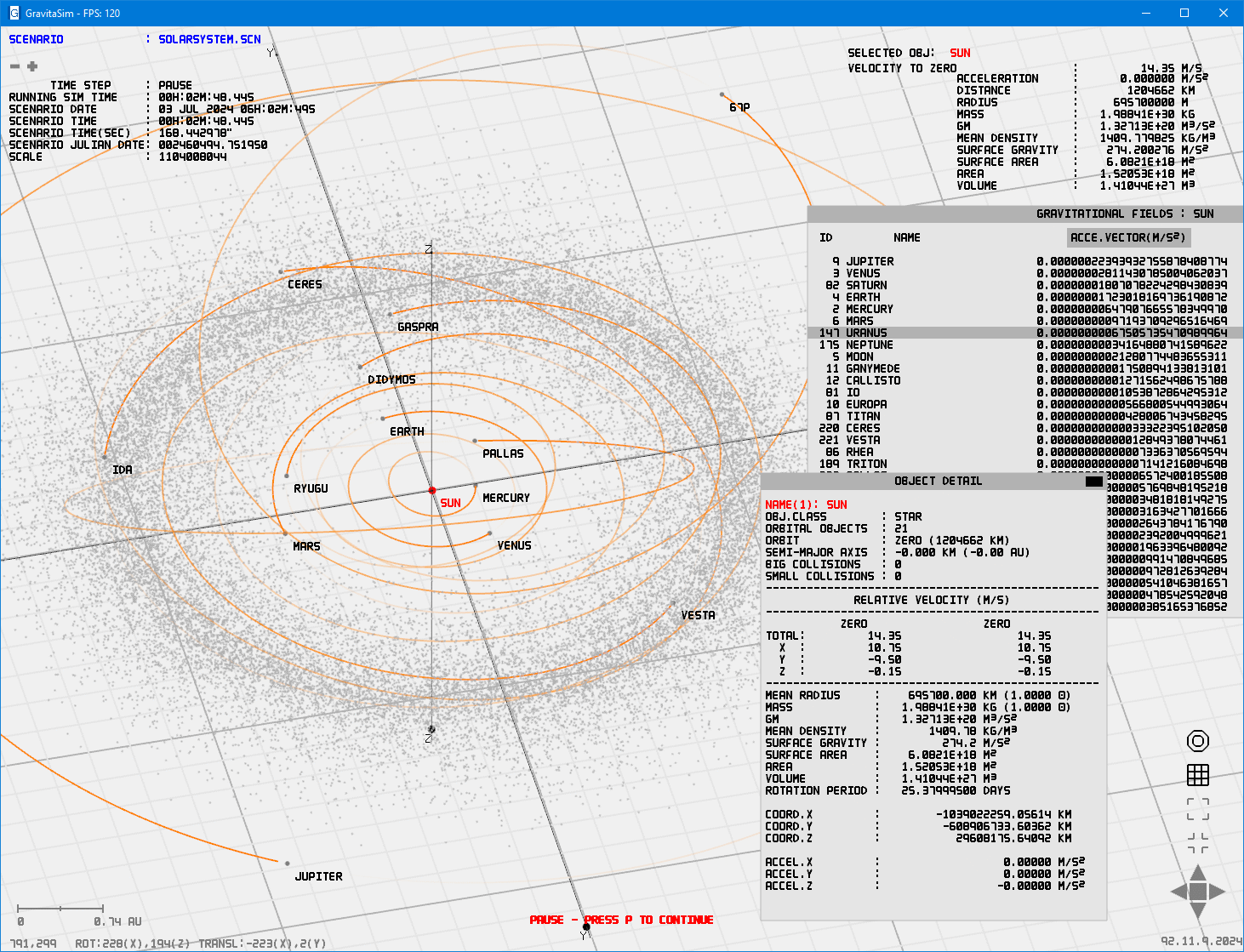
Asteroides troianos de Júpiter e os Pontos de Lagrange
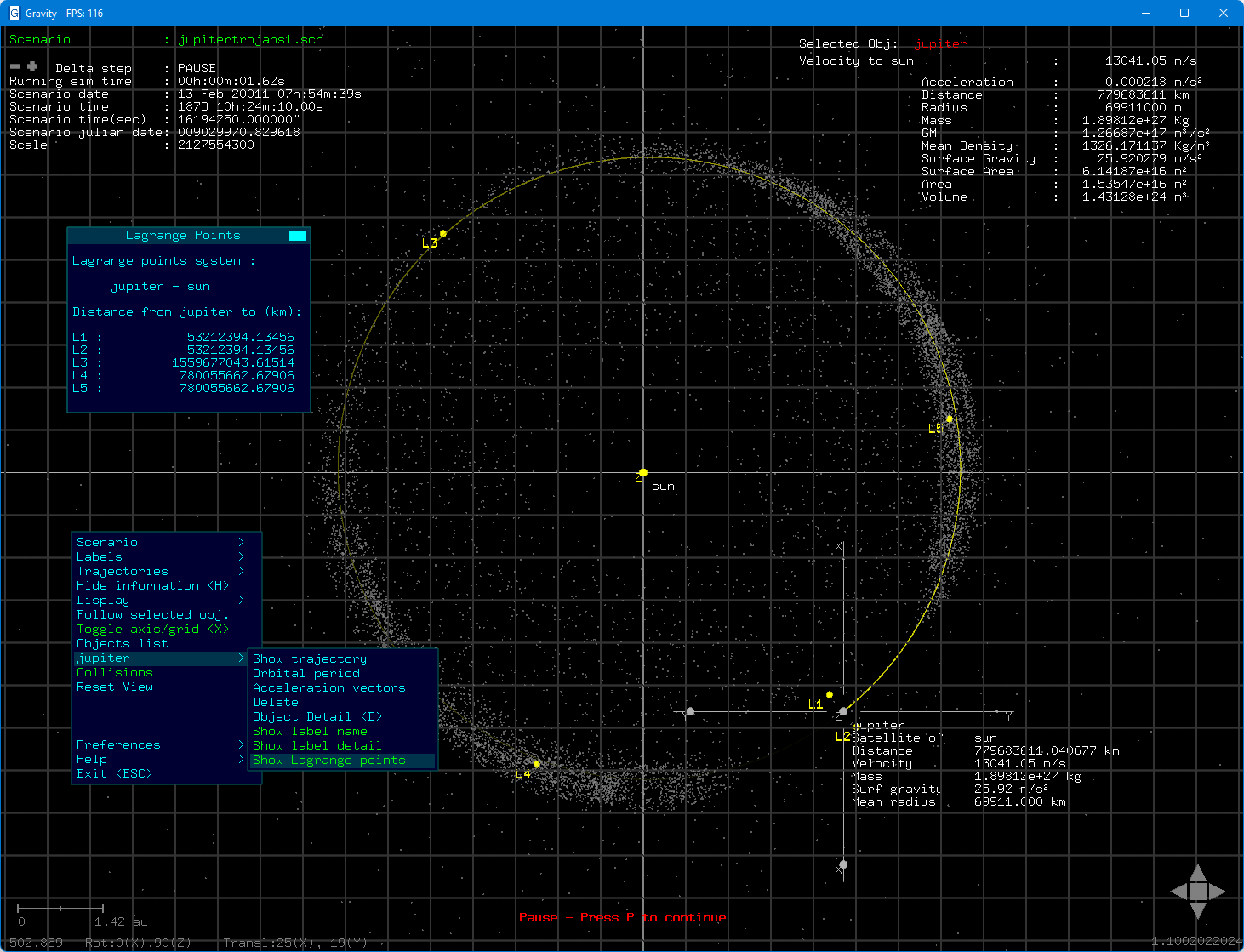
Aprendeu na escola que apenas os planetas se movem? Que as estrelas são imóveis? Estava errado. A trajectória do nosso Sol deslocando-se aproximadamente a 48 km/h devido à influência gravítica dos planetas do sistema solar.
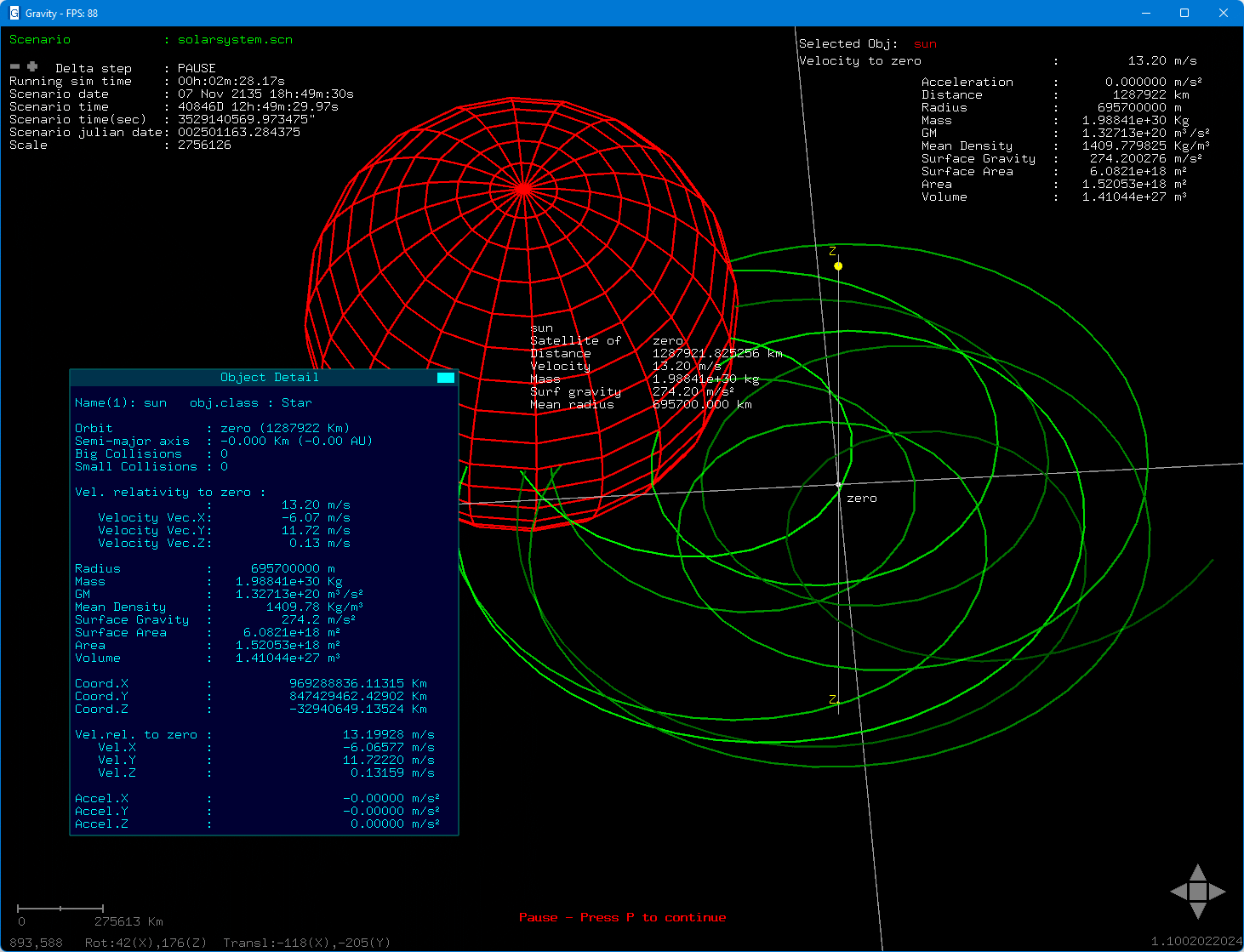
A detecção deste movimento oscilatório que algumas estrelas têm, é uma das técnicas usadas pelos astrónomos para detectar exoplanetas (planetas de outros sistemas solares da nossa galáxia).
Navegação com o rato
Os comandos do rato estão sintetizados nas seguintes tabelas e usam as seguintes abreviações:
| BER | Pressionar botão esquerdo do rato. |
| BMR | Pressionar botão do meio do rato. |
| BDR | Pressionar botão direito do rato. |
| Roda | Rolar a roda do rato. |
| Mover ecrã | BMR e mover o rato ou |
| SHIFT + BDR e mover o rato | |
| Aproximar/Afastar | Roda cima/baixo |
| Zoom in Automatico | Duplo click com BER |
| Rodar a imagem | BER numa área vazia do ecrã e mover o rato |
| Aceder ao menu principal | BDR numa área vazia do ecrã |
| Seleccionar objectos | BER no objecto a seleccionar |
Atalhos do teclado
Quase toda a interacção faz-se apenas com o rato, no entanto os atalhos do teclado sendo uma alternativa, podem ser efectivamente mais rápidos e convenientes.
| Rodar a imagem | Teclas do cursor |
| Aproximar | Tecla + do teclado numérico |
| Afastar | Tecla - do teclado numérico |
| Sair da simulação | ESC |
| Carregar novo cenário | L |
| Lista de todos os objectos do cenário | O |
| Interromper/Continuar a simulação | P |
| Reler o cenário | R |
| Reinicializar vizualização | V |
| Activar/Desactivar trajectórias | T |
| Activar/Desactivar informação suplementar | H |
| Activar/Desactivar Eixos | X |
| Detalhe do objecto seleccionado | D |
| Aumentar o Delta T | = |
| Diminuir o Delta T | - |
| Activar/Desactivar ecrã completo. | F |
| Zoom in Automatico | Z |
|
| |
| No contexto das janelas : | |
|
| |
| Move uma página para cima | PgUp |
| Move uma página para baixo | PgDn |
| Move uma linha para baixo | Cursor para baixo/Roda para cima |
| Move uma linha para cima | Cursor para cima/Roda para baixo |
Lei Universal da Gravidade
In 1687, um físico e matemático inglês, Isaac Newton apresentou esta lei para explicar os movimentos dos planetas e das suas luas. A lei universal da gravidade de Newton descreve que qualquer partícula de matéria no universo atrai outra com uma força directamente proporcional ao produto das suas massas e inversamente proporcional ao quadrado da distância entre elas.
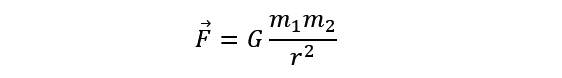
F é a força gravitacional, G é a constante gravitacional, m1 e m2 são as massas, e r é a distância que as separa.
Vejamos o exemplo clássico entre a Terra e a nossa Lua (consideraremos 384000km como a distância média entre os dois):

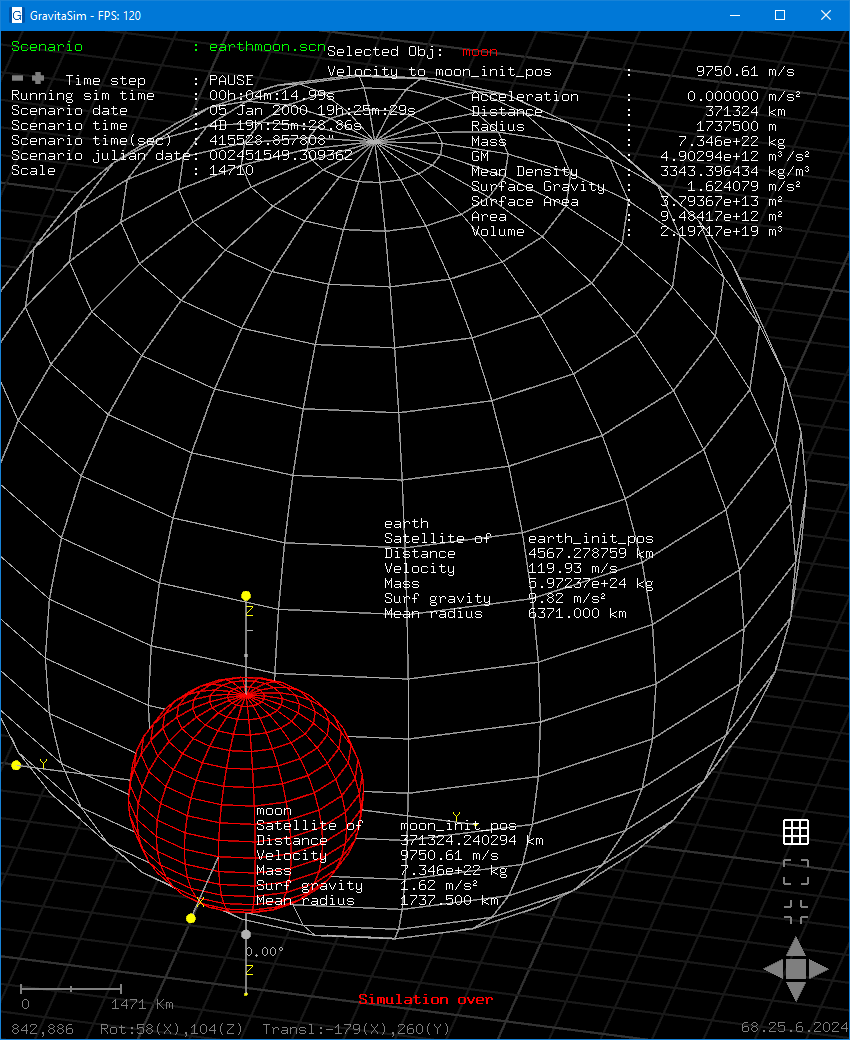
E se a Lua estivesse a cair em direcção à Terra?
No cenário “earthmoon.scn” foi criada uma situação em que a lua parou de orbitar a terra e está em queda livre na direcção no nosso planeta.
- Quanto tempo demoraria a Lua a atingir a Terra?
- Qual a velocidade da Lua ao atingir a Terra?
- Qual a velocidade da Terra no momento do embate?
- Que distância percorreriam a Lua e a Terra?
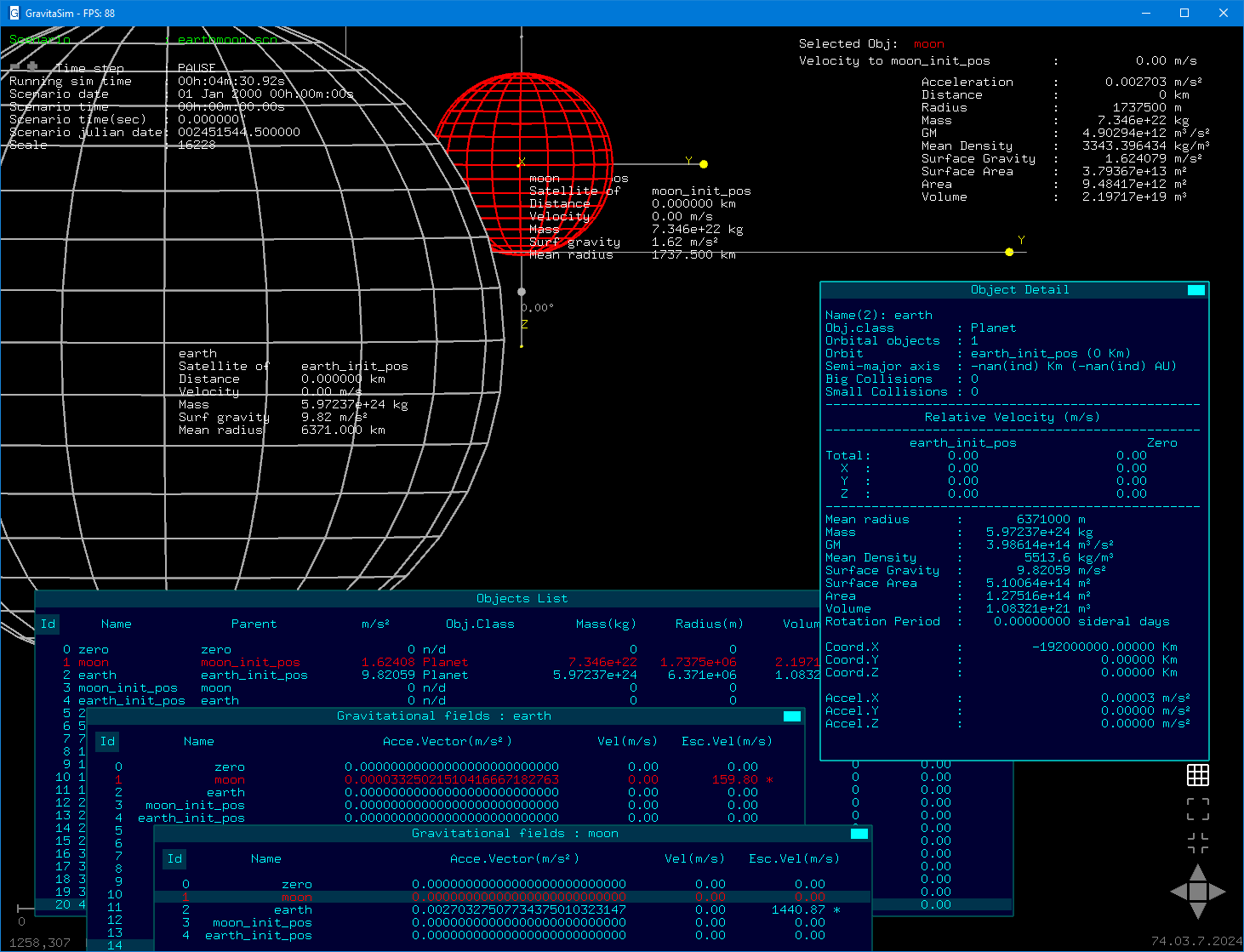
No momento do impacto, a velocidade de aproximação entre a Terra e a Lua seria de 9870 m/s (35533km/h)
A Terra e a Lua estariam a deslocar-se respectivamente com uma velocidade de 119.93m/s (431.7km/h) e 9750m/s (35100km/h).
O tempo necessário para o impacto seria de aproximadamente 4 dias 19 horas e 25 minutos. Durante este período de tempo a Terra percorreria 4567km. E a Lua os restantes 371324km
Downloads
Se está a actualizar GravitaSim, certifique-se que a pasta dos cenário foi apagada.
A nova versão pode não ser compatível com cenários antigos.
Comentários ou sugestões
Aviso: Todo e qualquer texto publicado na internet através deste sistema não reflecte, necessariamente, a opinião deste site ou do(s) seu(s) autor(es). Os comentários publicados através deste sistema são de exclusiva e integral responsabilidade e autoria dos leitores que dele fizerem uso. A administração deste site reserva-se, desde já, no direito de excluir comentários e textos que julgar ofensivos, difamatórios, caluniosos, preconceituosos ou de alguma forma prejudiciais a terceiros. Textos de carácter promocional ou textos inseridos no sistema sem a devida identificação do seu autor (nome completo e endereço válido de email) também poderão ser excluídos.